We may study the scientific aspect of soccer and thereby increase our understandings on this sport. Here, let us study the basic facts and principle of soccer by scientific analysis.

The Soccer Ball

"There can be no game of football without a ball and the better the ball, the better the game." [i]

The birth of contemporary football can be traced back to the 19th century. It began in 1863 in England when the world's first football association --- The Football Association in England --- was founded. At that time, most of the soccer balls were made of pig or ox bladder encased with leather. The major deficiencies of these balls were the difficulty of making a regular shape ball and maintaining the shape of the ball when use.

The first vulcanized rubber soccer ball designed and built in 1855 by Charles Goodyear [ii]

By 1900s, most balls were made of rubber bladder instead of the animals bladder while leather was still used as the covering material of balls. The use of the rubber bladders is to ensure that the ball can remain hard and avoid losing its shape. Thus these balls would bounce easier and yet could be kicked. However, leather will absorb water if it is wet. Therefore, the leather casing ball would absorb water during rain and become very heavy, which caused many head injuries at that time.

1910 soccer ball [ii]

1950 soccer ball [ii]

2004 Euro Cup ball [ii]

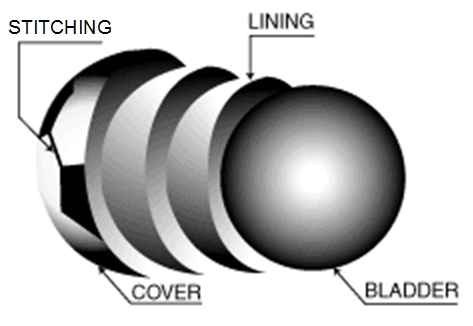
In the late 1980s, the leather casing ball was replaced by totally synthetic ball in soccer competitions. The covering material of the totally synthetic ball is synthetic leather made from polymer. For high quality ball, the casing is made of the synthetic leather panels stitched together through pre-punched holes by waxed threads. The bladder of a totally synthetic ball is usually latex or butyl bladder. The ball is then inflated by pumping air into its bladder through a tiny hole on the casing. The totally synthetic ball could resist water absorption and reliably maintain its shape.

The Internal structure of a totally synthetic soccer ball [ii]

Nowadays, the official soccer rules called the "Laws of the game", which are maintained by the International Football Association Board (IFAB), specify the qualities of the ball used in soccer matches. According to the laws, the soccer ball should satisfy the following descriptions:

• it is spherical in shape,
• its casing is made of either leather or other suitable material,
• its circumference is not more than 70 cm and not less than 68 cm,
• its weight is not more than 450 g and not less than 410 g at the start of the match.
• its pressure inside equal to 0.6 - 1.1 atmosphere at sea level.

How Things Work

Air pressure (Courtesy NASA) (Courtesy: xi) Air is consisted of a number of tiny particles called air molecules. By definition, pressure is the average amount of force exerted on unit area of a surface by a fluid. Thus air pressure tells us how much force the air molecules pushed on a fixed region of an object's surface that is surrounded by the air. Air molecules are not stationary and they move in random directions with a typical speed greater than that of a jumbo jet. Due to the random motion, the molecules continually bombard with each other. Moreover, the air molecules would hit and thereby exert force on the surface of any object exposed in the air which gives rise to the air pressure. In the "Laws of the game", "pressure" stands for the air pressure inside the ball. And "atmosphere at sea level" refers to the amount of force that the air in the Earth's atmosphere is pressing against us at the altitude of 0m, which is equal to about 10 newtons per square centimeter. For a surface of 1 square meters large, the force is about 100000 newtons which is equal to the weight of a bus! Why do our ears pop during the take-off? During the take-off of a plane, we often feel our ears painful and then our ears pop. We may have similar experience when we are on a high mountain. Explanations At higher altitudes, the number of air molecules per unit volume of the air is less than that at lower altitudes. If we reach a high altitude destination, the air pressure outside our eardrum decreases as there is less number of air molecules surrounding us. However, the pressure inside our eardrum would not change since our ears are sealed off inside our head. Thus, as the plane ascends or descends, the pressure inside our eardrum is greater than that outside which makes us feel painful. In order to equalize the pressure inside the eardrum, we need to open the Eustachian tube that connects the middle ear to the open area behind the nose. It is the opening of the Eustachian tube which gives rise to the "pop" sound we hear. Insight We may also feel ear pops due to the change in air pressure in case of --- riding on an express elevator to the top floor of a high building, --- diving to the bottom of a swimming pool. Obviously, a good soccer ball should not be too heavy to kick, or so light that it will not carry while it should not be too large or too small to control. In fact, the weight and size of the soccer ball defined by the "Laws of the game" agree closely with the requirements of a good soccer ball found by trial and error. The dimensions of different types of balls Ball mass, g diameter, cm Soccer 410 - 450 21.6 - 22.3 Golf >45.93 >4.267 Tennis 56.0 - 59.4 6.541 - 6.858 Basketball 570 - 670 23.9 - 24.8 Baseball ~150 ~7.48 The pressure of the soccer ball defined in the "Laws of the game" is unexpectedly low. In fact, the ball would collapse if its inside pressure is smaller than one atmosphere. And the ball is not hard enough even at a pressure of 1.1 atmosphere. The true meaning of the rule is a pressure difference between the inside and outside of the ball. Figure explaining the extra pressure inside the soccer ball. How to make a ball with extra air pressure inside? The extra air pressure is attained by pumping extra air molecules into the ball. Then there would be more air molecules in each unit volume of space inside the ball. As a result, the number of air molecules pushing the casing of the ball outward would be more than that pushing inward for each unit area of the ball's surface. Such imbalance of force leads to the pressure difference between the inside and outside of the ball. Why do some soccer balls expands over time? Many soccer balls become bigger after being used for a long time. Why? Explanations In the ball's bladder, air pushes against the linings and covering by exerting pressure on them. After the ball being used for a long time, it is probable that the material and stitching of the cover and linings stretch out. Moreover, overuse of soccer ball may also result in loosen stitching. Thus the cover and linings become less capable of resisting the pressure of the air inside the bladder. Hence, the ball would expand over time. Bouncing of ball If a soccer ball is dropped on a hard surface, it will bounce back to a height lower than its initial position. Such kind of motion is called the bouncing of the soccer ball, which plays an important role in the motion of the ball. Let us study the mechanism of the bouncing of the ball in details. The relative bounciness of different types of balls [iii] In fact, the mechanism of the bouncing of different kinds of spherical balls are similar and thus we can study the bouncing of a spherical ball instead of soccer ball only. However, different types of balls have different bounciness (different bouncing abilities), as shown in the above chart. For example, the baseball is less bouncy than the soccer ball, i.e. the baseball will bounce back to a much lower position than the soccer ball if they are dropped from the same height. Why some balls are bouncy while some others are not so bouncy? It is determined by the elasticity of the ball. A more elastic ball has more bounciness. 1. Elasticity of the ball The elasticity of an object means the tendency of the object to return to its equilibrium shape, the natural shape of the object with no net force applied on it, when it is being deformed. And the force for the object to restore to its equilibrium shape is called the restoring force, which is always directed in opposite to the deformation of the object. Almost all real rigid body are elastic, i.e. having certain extent of elasticity. A trivial example of an elastic object is the spring. You probably have the experience that a spring would tend to restore to its original size when you stretch it to be longer. Scientist found that, providing the deformation is not too large, the relationship between the distortion and the restoring force is given by the Hooke's law: "The restoring force exerted by an elastic object is proportional to how far it has been distorted from its equilibrium shape." The restoring force Fs on a spring in case of different extension. Note that the Hooke's law no longer holds if the object is distorted too much that it has been permanently deformed. Work must be done in order to distort an elastic object. Therefore, if you pull a spring outward so that it become longer, some energy must have been transferred from yourself to the spring. The energy stored in an distorted object due to its deformation is called the elastic potential energy. So, when talking about the elasticity of the ball, we are indeed talking about the spring-like behavior of the ball. In other words, we are considering the tendency of the ball to return to its original spherical shape when it is being squeezed. Where does the elasticity of the ball come from? The elasticity of a solid ball arises from the elasticity of the constituting material which is due to the interatomic or intermolecular force inside. In contrast, for air-filled ball like soccer ball, its elasticity is resulted from the extra air pressure inside the ball. What happens to a ball after you dropped it above a hard floor? The gravity pulls the ball toward the ground and thus the ball falls leading to the lost of its gravitational potential energy. By the law of conservation of energy, the ball must gain kinetic energy and so it falls towards the ground with an increasing speed. Subsequently, the ball hits the hard floor with a high speed. (Note that the ball always moves with the downward acceleration of g = 9.8 m/s2 as it falls.) Energy change in the falling ball after release until hitting on the ground. (Note that here "G.P.E." and "K.E." stand for the gravitational potential energy and kinetic energy respectively.) 2. Law of conservation of energy In the law of conservation of energy, it was stated that: "Energy can neither be created or destroyed but can only be changed from one form to another." Therefore, the amount of total energy in an isolated system must be constant. For example, let us consider a piece of charcoal placed in an isolated room. If we burn the charcoal, the chemical energy inside the charcoal is changed into the thermal energy of the room. Then the temperature inside the room would be increased. When the ball hits the ground, the ball exerts force on it. By the Newton's 3rd law of motion, the ground exerts a force on the ball as well. The motion of the ball would be stopped by the (stationary) hard floor resulting in the compression of the ball. So the work done on the ball leads to the increase of the elastic potential energy of the ball. That means some of the kinetic energy of the ball (which is converted from the gravitational potential energy of the ball) is converted into the elastic potential energy when the ball hits the ground. On the other hand, some of the kinetic energy is lost as thermal energy during the impact due to either the internal friction of the ball or the heating of the surface. Energy change in the falling ball during the impact After losing all the kinetic energy, the ball becomes momentarily at rest. The squashed ball would simply act like a compressed spring. The ball pushes the ground with a restoring force proportional to its displacement from the equilibrium position (Hooke's law). In consequence, the ground pushes back the ball with a force of equal magnitude but opposite in direction. Thus the ball bounces back in upward direction. During the rebound, the stored elastic potential energy is released as the kinetic energy of the ball which is then converted to gravitational potential energy as the ball moves up. Moreover, some of the elastic potential energy is lost again due to friction or heat which results in slight heating of the ball. The ball keeps on going upward until it comes to rest after losing all its kinetic energy again. Due to the lost of some of the initial gravitational potential energy into thermal energy, the ball cannot bounce back to the original height. Energy change in the ball during the rebound. (Note that here "E.P.E." stands for the elastic potential energy.) The path of a bouncing tennis ball [iv] Chart of energy conversion in the ball from falling to rebound. The net effect of the bouncing of the ball is that the kinetic energy before the impact must be larger than that after the impact. That's why it is impossible for a ball to be perfectly elastic, i.e. retaining all the kinetic energy before the impact. In fact, the loss of the kinetic energy would be smaller for a more elastic ball. Thus the elasticity of a ball can be measured by the ratio of the speed of the ball before and after the impact which is called the coefficient of restitution e: Note that the coefficient of restitution is larger for a more elastic ball. The coefficient of restitution would be equal to one for a perfectly elastic ball bouncing on a hard surface while it is equal to almost zero for a putty ball. For a typical soccer ball hitting on a hard floor, the coefficient of restitution is about 0.8 and thus its speed would be reduced by 20% after the impact. The table below summarized the coefficient of restitution of different types of ball. Approximate coefficient of restitution for different types of balls type of ball coefficient of restitution Superball 0.9 Tennis ball 0.75 Baseball 0.55 Foam rubber ball 0.30 Beanbag 0.05 It can be shown that the coefficient of restitution is also proportional to the ratio of the drop height to the rebound height: The path of the bouncing ball for different coefficient of restitution (C.O.R.) where e1 > e2. As a result, a ball with smaller coefficient of restitution rebounds to lower height in successive bounces and a shorter time is required for the ball to stop (see below figure). For example, grass reduces the coefficient of restitution of a soccer ball since the bending of blades causes further loss of its kinetic energy. Therefore, it would take a shorter time for the soccer ball to stop if it is kicked on grass instead of hard floor. 3. Experiments of bouncing balls Measuring the bounciness of a ball is not difficult. We can measure it by dropping the ball from a height onto a hard surface and observing how high it bounces back. The ratio of the height from which you dropped it (drop height) to the height of the first bounce give us a measure of the ball's bounciness. We can also change the bounciness of a ball by changing its temperature. Take two baseballs that bounce to about the same height. Put one in the freezer for an hour and leave the other at room temperature. Then compare their bounciness again. You should notice that the room temperature ball bounces a little bit higher. The cold ball would bounce about 80 percent as high as the room temperature ball. Although the difference of bounciness is not dramatic, it's enough to see that temperature can be a factor: it could make the difference between a home run and a pop fly. Comparing the bounciness of frozen and room temperature baseballs (the left picture) and golf balls (the right picture). In both pictures, the room temp. balls are on the right . [iii] If we repeat the above experiment for two golf balls, we would find that the refrigerated ball should bounce about 70 percent as high as the one at room temperature. That's why some golfers put their spare balls in their pockets on cold days since they want to avoid the ball losing its bounciness by keeping the temperature of the balls. However, the change in bounciness due to the change in temperature is taken for granted for some sport. For example, squash player rely on the pre-game warm up to warm up the ball as well as the players.

Flight of Ball in Air

Suppose a soccer ball is kicked and then flies into the sky with no spin. It then travels through the air before touching the ground. However, the air resists the ball to move through it. Thus the horizontal displacement of the ball in air would be much shorter than that in case of vacuum. For example, a soccer ball kicked without spin at a speed of 35 m/s and at an angle of 45 degrees to the ground would transverse a horizontal distance of 66m in air; while the distance would be 125m in vacuum. This example clearly illustrates the importance of air resistance in the motion of the ball. So let us investigate how air affects the flight of a ball.

When a ball is moving through the air, it experiences a drag force exerted by the passing air. For simplicity, we study this problem by taking the ball being stationary with air flowing over it. Indeed, there are two types of airflow, known as laminar airflow and turbulent airflow, whose behavior are remarkably different. In laminar airflow, viscosity dominates the flow, keeping it smooth and orderly; while in turbulent airflow, inertia dominates the airflow, ripping it apart into swirling eddies. Whether the airflow is laminar or turbulent depends on the size of the obstacle that the air encounters and the speed of the air passing the obstacle.

How Things Work

1. Viscosity of air In fluid including air, there is viscous force opposing the relative motion of different layers of fluid and producing friction-like effects within the fluid. Viscosity is the measure of this resistance to relative motion within a fluid. We can see that the honey is much more viscous than the red solution You can observe this effect when you pour honey out of a jar. The honey near the jar's wall is stuck there and can't move. But even honey that's far away from the wall can't move easily. It is because the viscous force within the honey try to prevent any of the honey moving since the honey near the wall can't move. Of course, the viscosity of the air is much lower than that of the honey. Different fluids have different viscosity. For example, the viscosity of the air is much lower than that of the honey and water. 2. Laminar airflow for a slow-moving ball Let us first consider a ball moving slowly through the air. If the ball moves slowly enough, the airflow is laminar. The below figure shows the laminar airflow around a slow-moving ball. In the figure, the lines indicating the airflow, along which each small piece of air follows, are called the streamlines. For laminar flow, the air between two streamlines remains between those streamlines throughout its motion. 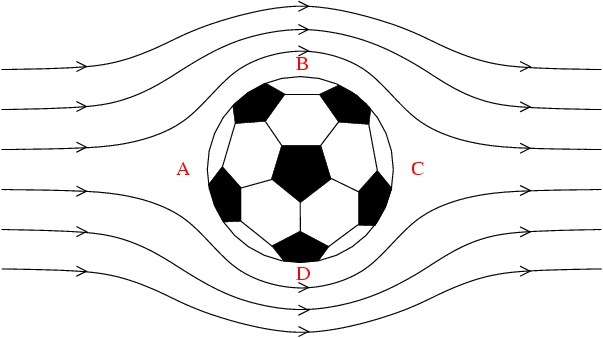The airflow pattern around a soccer ball in case of laminar airflow. Since the flow is laminar, the air separates neatly in front of the ball and then recombines again after passing the ball, leaving a smooth and free-of-turbulence wake --- an air trail left behind the ball. So the streamlines bend outward on approaching the ball (point A) and bend inward again on leaving the ball (point C). There must be change in air's speed and pressure so that the air can change its flowing direction. Specifically, air experiences a drop in speed and a rise in pressure in the region where it bends away from the ball's surface (near point A and C); while air experiences a rise in speed and a drop in pressure in the region where it bends toward the ball's surface (near points B and D). Thus, as indicated by the widely spaced streamlines, the air moves slower at the high-pressure region near the front and back of the ball (points A and C). Moreover, at the low-pressure region near the sides of the ball (points B and D), the air moves faster as indicated by the narrowly spaced streamlines. It is consistent with the Bernoulli's principle that the speed of a stream of moving fluid will increase if it flows into a narrower channel where the pressure is decreased. 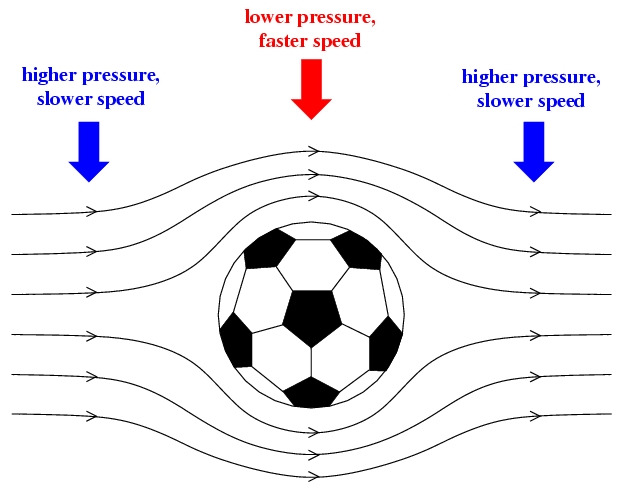The pressure and speed of the air flowing at different region around a soccer ball. It may seem strange that why the air can flow from the low pressure region near the sides of the ball to the high pressure region at the back of the ball. It is because the low-pressure air sweeping the sides of the ball have enough forward momentum (= mass x velocity) to move to the back of the ball. Thus the airflow slows down when it move from the low pressure region to the high pressure region. Although there is change in the speed and pressure of the air on moving past the ball, the airflow is symmetric and the forces exerted by the air pressure are also symmetric. The high pressure in front of the ball is balanced by the high pressure at the back of the ball. Thus the pressure forces cancel out completely and so the ball experiences no net pressure force. As a result, the only force that the passing air acting on the ball is the viscous drag - the friction-like downstream force due to the sliding of the viscous air across the ball's surface. 3. Turbulent airflow for a fast-moving ball When the ball moves faster, the airflow become turbulent. Unlike in laminar flow, the air pressure is not distributed symmetrically around the ball in the turbulent flow. Thus the pressure forces cannot balance with each other and the ball experiences pressure drag - downstream force exerted by unbalanced pressures in the moving air. In other words, it is the imbalance pressure which slows down the motion of the ball in turbulent airflow. The airflow would become turbulent so that the ball would experience pressure drag when the Reynolds number exceeds about 2000. Thus the Reynolds number gives an indication whether the airflow is turbulent or laminar. Researchers showed that the Reynolds number depends on the ball's size and speed as well as the viscosity and density of air. At low Reynolds number, the air's viscosity supports laminar flow over the ball's surface. At high Reynolds number, the air's inertia prevents it curving around the ball's surface and air's viscosity triggers the air to swirl about. 4. The Reynolds number To figure out a fluid flow is dominated by inertia or viscous force, physicists tell us that we need to consider the following quantities related with the fluid and its environment: The viscosity of the fluid. High viscosity favors laminar flow because viscous forces tend to keep nearby regions of fluid moving together. The speed of the fluid flowing past an obstacle. If the fluid is moving past the obstacle with a faster speed (relative to that of the surface in contact on the obstacle), any two nearby regions of fluid will separate much more rapidly and thus it is less likely for these fluid to be kept moving together by the viscous force. The size of the obstacle encountered by the fluid. It is more probable for a larger obstacle to cause turbulence since viscous force cannot keep the fluid flowing in order over a very long distance. The density of the fluid. Denser fluid has less response to viscous force than dilute fluid. Therefore, it is more likely for the dense fluid to become turbulence as it flows. It is troublesome to consider the above four quantities one by one in determining whether the fluid flow is laminar or not. In view of this, the English mathematician and engineer Osborne Reynolds (1842-1912) defined the Reynolds number by combining these four quantities as follows: By calculating the dimensionless Reynolds numbers, we can estimate whether the flow of a fluid is laminar or turbulent. How the air's viscosity triggers the swirling air in turbulent flow? We have to look at the air near the ball's surface. Viscous force within the air keeps the air touching the surface to remain at rest and also slows down the nearby air to form the boundary layer. In the boundary layer, the air moves more slowly and have less total energy than the freely flowing air farther away from the ball. Outside the boundary layer, the viscosity of the air can be neglected. 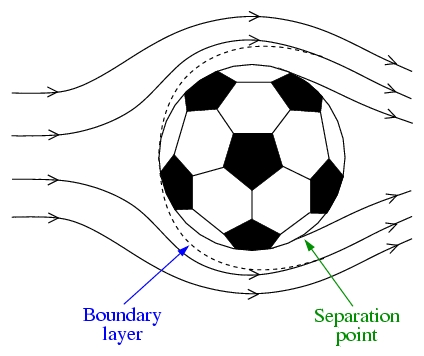The boundary layer around a fast-moving soccer ball. When the air flows toward the back of the ball, it travels from a low pressure region to a high pressure region. Although the air outside the ball have enough total energy to reach the back of the ball under the unfavorable pressure change, the air in the boundary layer does not. At high Reynolds number, the viscous forces between the freely moving air and boundary layer is not strong enough to push the boundary layer moving to the back of the ball. Eventually, the boundary layer stops and reverses directions. The airflow would be messed up by this boundary layer reversal that the freely flowing air separates from the surface and the separated airflow produces eddies behind the ball. These eddies are then confined together to form a turbulent wake similar to that left behind a ship moving through the water. 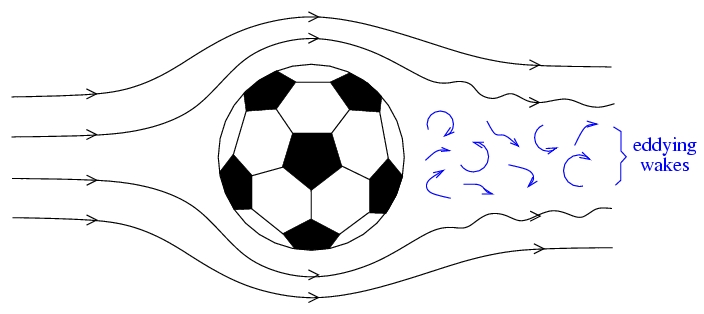Eddying wakes are formed after a fast-moving soccer ball. Because of this turbulent wake, the air behind the ball no longer slows down and its pressure no longer rises. Thus the air pressure in front of the ball is higher than that behind the ball. Hence, the ball experiences pressure drag pushing it backward for turbulent airflow. The pressure drag is the main source of the drag experienced by a ball moving through the air for turbulent airflow. Alternatively, we can say that the slowing of the ball is due to the loss in the kinetic energy of the ball for the extra kinetic energy of the eddying air in the turbulent wake. 5. What will happen for a very-fast-moving ball? If the speed of the ball is further increased, the freely moving air will separate from the ball's surface earlier since the Reynolds number increases further. That is to say, the separation points move to a more upstream position. As a result, the turbulent wake become wider resulting in a greater pressure drag on the ball. In brief, the air drag will increase if the speed of the ball increases for a fast-moving ball. However, if the speed of the ball is increased so much that exceeding the critical speed, the drag forces would behave in a very different manner as a function of the air's speed. When a ball travels fast enough that its Reynolds number exceeds about 100000, the boundary layer itself also becomes turbulent. Since the air in the turbulent boundary layer have more kinetic energy than that in the laminar boundary layer, the turbulent boundary layer can move to a farther position at the back of the ball before stopped by the rising air pressure. Thus the freely flowing air outside the turbulent boundary layer would separate at a more downstream position leading to a smaller wake and reduced drag. So there is a sudden drop in air resistance when the boundary layer changes from being laminar to turbulent. 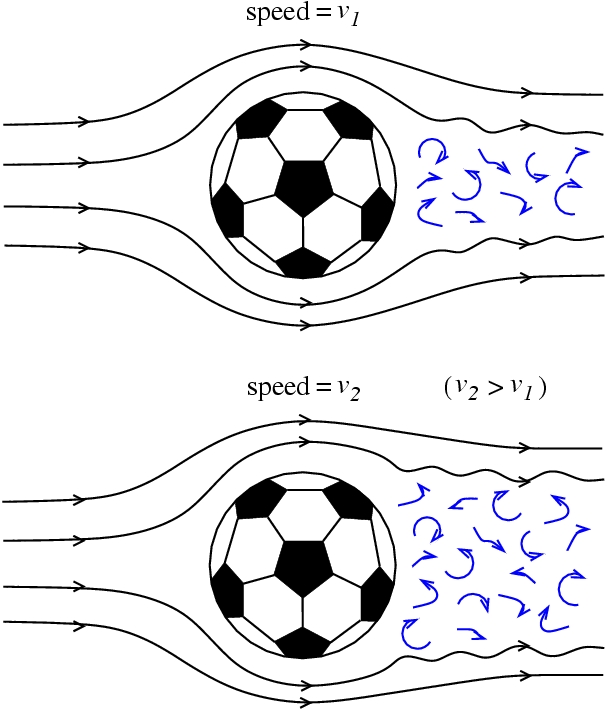Eddying wakes formed after a soccer ball would be larger if the ball moves with a faster speed. Note that both v1 and v2 are smaller than the critical speed. 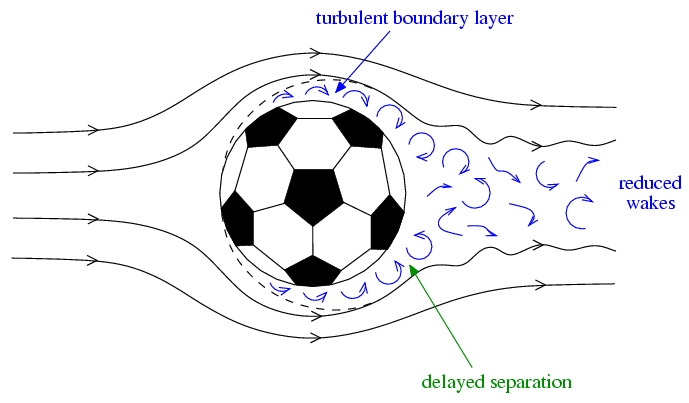The turbulent boundary layer gives rise to a reduced drag if the ball's speed exceeds the critical speed. The critical speed is defined to be the speed of the ball at which the boundary layer become turbulent and thus the air drag is reduced. Above the critical speed, the drag force falls with increasing speed until it exceeds another critical value. From the below figure, we can see that the critical speed of the soccer ball is around 20 m/s. The air drag on a soccer ball as a function of its speed [v]. Any seams or irregularities on the sphere could "encourage" the formation of a turbulent boundary layer around the ball. For such case, the critical speed would be reduced and thus the air drag would be less for a fast moving ball with rough surface. That's why a tennis ball has fuzz and a golf ball has dimples. In summary, we have found that the air flowing around a non-spinning ball moving through the air exhibits different properties in case of different Reynolds number as summarized in the table below. As a result, the air drag experienced by a ball has different characteristics if the ball moves with different speed. Airflow around a ball for different Reynolds number Reynolds number Boundary layer Type of wake Main drag force <2000 Laminar Small laminar Viscous 2000 - 100000 Laminar Large turbulent Pressure >100000 Turbulent Small turbulent Pressure

Curving of Ball in Air

How Things Work

In the previous section, we have investigated how the air drag affects the motion of a soccer ball traveling through the air. Indeed, air drag is not the only possible force exerted by air sweeping past a moving ball. It is also possible for the passing air to exert lift forces acting perpendicular to the airstream on a moving ball. Unlike drag force, lift force pushes the ball sideway to either upward or downward directions which causes the ball to curve in flight. Bend it like Beckham The path of a banana shot kicked by David Beckham [vi]. The "banana shot", a ranged shot curling on its way to the goal, is a very useful trick for deceiving the defensive walls and fooling the goalkeepers so that the ball can score. In soccer matches, it's not rare for player to kick the "banana shot". For example, David Beckham is famous for being able to kick the "banana shot" to get score for his team. If you are careful enough, you probably notice that the ball is spinning in all the "banana shots". In fact, the ball must be spinning rapidly in order to produce a curved flight. The phenomenon that a rapidly spinning ball moving in air would be deflected by the resultant lift force to follow a curved path is called the Magnus effect. Let us take a look on how a spinning ball interacts with the surrounding air to give rise for the Magnus effect. Suppose a ball is kicked to rotate clockwise rapidly about an axis perpendicular to its moving direction during its motion to the left (see below figure). Then the ball would experience two lift forces, the so-called Magnus force and the wake deflection force, pushing it upward when it travels through the air. Thus the ball moves with a curved path to reach the goalkeeper's right. 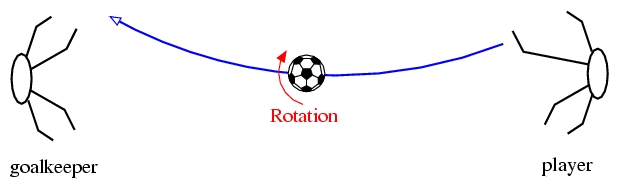A soccer ball is shot to spin clockwise during its motion to the goalkeeper. The Magnus force, discovered by the German physicist H. G. Magnus (1802 - 1870), is due to the interaction between the spinning ball and the viscous air. For a spinning ball, the passing air is moving in the same direction as the surface of contact on one side of the ball while it is moving in an opposite direction as the surface of contact on the other side. Therefore, the relative speed of the air is smaller at the side where it flows along with the rotating surface of the ball. Thus the Reynolds number is also smaller at this side. Hence, as explained above, the viscous air will separate from the ball's surface at a more downstream position on the side that the air moves in the same direction as the rotating surface. In contrast, on the other side of the ball, the point of separation is much earlier because the Reynolds number is larger over there. (Of course, we have assumed that the relative speed of the air does not exceed the critical value on both sides of the ball.) As a result, the airflow pattern around the spinning ball is not symmetric. The moving direction of the airstream is twisted to the side that the air moves opposite to the rotating surface. Moreover, the turbulent wake is also deflected toward this side. According to the Newton's 3rd law of motion, there is a reaction force that the ball pushes the airstream as well as the turbulent wake to the opposite side. The Magnus force is the resultant sideway reaction force due to the deflection of the air flow while the wake deflection force is the resultant sideway reaction force due to the deflection of the turbulent wake. The below figure illustrates how these two force arisen for a spinning soccer ball. 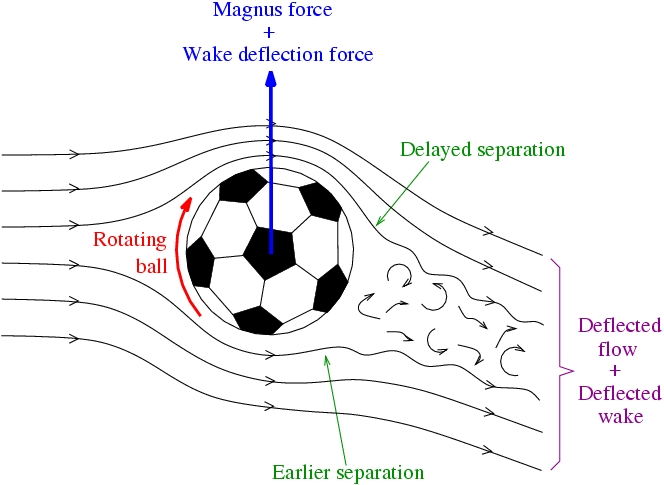The Magnus force and wake deflection force on a soccer ball which is spinning clockwise. We should remind that both the Magnus force and the wake deflection would deflect the spinning ball to the same direction. Besides, it can be shown that these lift forces would be maximum if the axis of rotation of the ball is perpendicular to the line of motion of the ball while these forces would be zero if the axis of rotation is parallel to the line of motion.

Physics of Injuries Caused by Collision

Preliminary knowledge

Almost everybody would agree that the aim of every sport player is winning the game through competitions. Thus, collision occurs frequently in many sport competitions including soccer matches. For example, a soccer player's feet hit the ground when he/she runs on the field. It is also not rare that a soccer player carrying the ball to approach the opponent's goal smashes with the defending players of the opponent's team. In addition, player sometimes gets score by using his/her head to hit the ball into the goal. However, if the collision is too strong, players might hurt by minor injuries like cuts, bruises, abrasions, sprains and twists. For more violent collision, players might have more severe injuries like broken clavicles, cracked ribs, torn knee alignments, smashed noses, fractured jaws, pulled muscles and so on. In the most severe cases, players might suffer from paralysis or death due to either broken spines, snapped necks or bleeding brains. A player may hurt if he strikes the soccer ball with his head [viii] In the last two decades, researchers have paid much efforts in developing sports medicine and protective equipment that prevent injuries and speed up athlete's recovery. However, even the most sophisticated medical techniques and equipment can't guarantee that an injured athlete can have total recovery. Therefore, it is necessary for us to learn how collisions are governed by physics and human physiology in order to avoid injuries in sport competitions such as soccer matches. What is the physics behind a collision? By the way, what is the use of physics in understanding the effect of a collision? In fact, physicists can tell us many information about a collision based on physical analysis. For example, they can tell us what really happens at the instance that the collision occurs. Besides, they can also calculate how much force and energy is involved in the collision. Using this information, we can estimate the chance for the player to get hurt in a collision. Suppose we want to find out how much energy involved in a collision between two American football players. According to physicists, the amount of energy involved in a collision only depends on how fast the players are moving and how much mass each player has. For ordinary people, it may seems that mass and weight are just the same thing. However, physicists point out that mass and weight indeed have different meanings. To understand the difference, we should remind that objects become weightless in outer space although they still have mass. Therefore, objects float inside a space shuttle moving in the outer space which we may see in TV news. How to measure the mass of a weightless object? We can do so by observing how much force is required to push the object at rest to start moving or how much force is required to stop the motion of the object. In other words, we can figure out how massive a weightless object is by measuring its inertia. But on the Earth, the weight of an object is proportional to its mass as indicated by physicists. That's why some ordinary people think that weight and mass have the same meaning. Although our body has mass, but we would become weightless under the zero-G condition. [vii] Once we know the mass and speed of a player, we are ready to calculate his/her kinetic energy which is the energy associated with one's motion. The kinetic energy of a moving player is just half of the player's mass multiplied by his/he speed squared. Alternatively, the kinetic energy is given by the formula: By the law of conservation of energy, energy can't be created or destroyed but only converted from one form to another. Now we have learnt how to find the kinetic energy of the American football players before their collision. Moreover, we know that the players' kinetic energy drop to nearly zero at the moment of collision since they don't move after the collision. Thus we can figure out how much energy is changed to another form during the collision. According to detail calculations as shown in the box below, it turns out that the energy of a collision between two American football players is big enough to lift a 23-ton block about an inch. In other words, this energy is sufficient to lift a compact car about two feet in the air. How energetic is the collision between two American football players? (Courtesy North Carolina State University) Answers In an American football match, player John runs head-on into the opponent's team player Peter when John is running up field. The loud sound of the bombardment of the helmets and bodies of the players echoes inside the stadium. How much energy is involved in this collision? To find the answer, we need to know how massive are the players and how fast they are moving at the instance of collision. Suppose it is given that the weight of John is 209 pounds and the weight of Peter is 247 pounds. For the calculation of energy, we have to convert their weights in pounds into mass in kilograms. Since one kilogram (kg) is equivalent to 2.2 pounds, the masses of the two players are equal to 95 kg and 112 kg respectively. Besides, suppose we found that the invading player John runs 8 yards in a second, which is the typical speed of a capable player. In metric units, this corresponds to about 7.3 meters/second (m/s). Moreover, the defending player Peter is assumed to be running at a slower speed of 6.2 m/s (which is about 7 yards in a second). During running, each player must possess kinetic energy, the energy associated with any motion, which is equal to 0.5mv2. Since both players are stopped by the collision, the total energy associated is the sum of the each player's kinetic energy. Physicists measure energy in unit of Joule (J). The calculation is as follows: Energy of John = 0.5 x 95 kg x (7.3 m/s)2 = 2531 J Energy of Peter = 0.5 x 112 kg x (6.2 m/s)2 = 2153 J Therefore, total energy involved in the collision = (2531 + 2153) J = 4684 J How big is this energy? It's big enough to lift a 23-ton block by one inch! If the duration of the collision is known, we can also find how powerful is this collision. The power is usually measured in unit of Watts where one Watt is equal to one Joule per second. We can find the power of a collision by dividing the energy of the collision by the time of the collision. For the collision between two football players, the collision lasts for about 0.3 second. Therefore, the power produced in this collision is given by: 4684 J/0.3 s = 14052 W which is equal to about 14 kilowatts. Such energy can power up 140 100-Watt light bulbs which are commonly used in household! As mentioned above, the energy of motion of the colliding football players must go somewhere since it is completely lost during the collision. Where does it go? That energy goes into the mighty deformation of the players and the heat energy dissipated by the rubbing of the players. How would the player affected by the energy of deformation? Besides the pain due to bodies' deformation, the players' bones might also be broken because of this energy. We should note that the deformation energy would still appears in the collision even the players don't stop moving after the collision. Thus we know that the injuries of players due to the collision on the football field depends on only two factors: the speed and mass of the bombarding players. We have learnt the approach to find the energy in a collision between two American football players. Similarly, this approach can be applied to any other sport that involves collision such as bats hitting the balls, feet colliding with pavement, feet hitting the soccer balls and so on. That is to say, what we need to know for finding the energy involved are the mass of the moving objects and the speed of their motion. We can take an alternative approach to analyze the collision between two football players. In such a collision, it almost always ends up with one person falling on the ground. That person isn't necessarily the one who moves slower or the one with the least mass. In fact, the person falling on the ground is the one who has the smallest linear momentum which is equal to the mass times the velocity. If the less massive player is moving very fast, he/she might have larger linear momentum than the other player. To change the linear momentum of an object, we have to apply force on it. Physicists tell us that how much force need to be applied depends on the linear momentum possessed by the moving object. For example, it's difficult to stop a steady moving luxury cruise (large mass; low velocity) or a 6-mm wide bullet (small mass; high velocity). Assume your teammate shot the soccer ball to you at a very high speed. For easy handling, you would like to stop the ball and thus reduce its momentum to zero before kicking the ball towards the goal or to another teammate. How do you do this? Obviously, you can apply a force on the ball in order to change its linear momentum. If you could only apply a small force on the ball, you have to apply it for a long time. But if you are strong enough to apply a much larger force, then you only have to apply the force for a short period of time. Why we have the choice? It is because of the quantities called impulse defined by physicists. Impulse measures the change in the linear momentum of an object. Physicists also showed that the impulse is simply equal to the applied force multiplied by the time that the force is applied. For the same change in momentum, a relatively less force would be required if the collision takes place over a longer time. That's why you would have less severe injury for falling on a pile of mattress than falling onto a concrete. It is because the pile of mattress would allow your body to slow down gradually (thus longer collision time) while the concrete would stop your body abruptly. Although the impulse are the same in both cases, the force applied on your body have a large difference. If you can't avoid colliding with something, you could reduce the extent of injury by increasing the time of collision which gives rise to smaller collision force. What would be the injuries caused by a collision? Collision often leads to deformation of the colliding object. And in sports, the object deformed is usually the human body. In fact, even the simplest collision can cause severe injury in your body. A foreign object hitting your body impacts a number of different structures. First, it can compress and activate nerve endings. Besides, the object can break the skin and then cause breeding by bursting the veins beneath the broken skin. It might also cause a bruise by bursting the veins without breaking the skin outside. Any damage in tissue would result in inflammation which is one of the self-defense mechanism of human body. If an area is inflamed, more blood would flow to the damaged tissue and thereby bring in the cells called phagocytes that destroy invading bacteria and any other foreign material by "eating" them. Phagocytes also prepare the repair of the damaged tissue. A collision can also cause stretching or tearing tendons, ligaments or muscles. It can also twist, unhinge or misalign a joint which is the most fragile structures in the human body. We are easily get injured by collision when we play sports. Any impact causing damage of tissue usually also causes pain. Obviously, different person have different responses even for the same pain. Dr. David Janda, who is an orthopedic surgeon of the institute for Preventative Sports Medicine, thinks that some of this difference may be physiological - but a lot is psychological. Dr. Janda says, "There are pain fibers and it seems that some people have more pain fibers or more hyper-reactive pain than others. But pain also has a psychological component. Some people come into my office and they say, 'hey you know this isn't so bad.' Others come in with the same injury and they're writhing and screaming. Some of it is attitude. Some of it is what we call 'secondary gain,' or people who get something else out of their pain, like attention. And some people panic when they have pain, which makes the pain even worse." Another factor that affects the degree of damage and pain due to a collision is the pressure which his the force per unit area. It was found that a large force distributed over a large area will cause less damage than the same force concentrated in a small area. What is the similarity between a karate strike and a woman in high heels standing on grass? The similarity is that the force is focused on a small area in both cases. Since most of the weight of the woman in high heels is pushing on a small point, the spikes of the high heels sink into the grass. If she wears running shoes instead of high heels, she would not sink into the grass as her weight now spreads over a larger area. Similarly, by striking with the edge of the hand, a karate black belt maximize the damage at the point of contact by focusing the striking force on a small area. To reduce the degree of damage, protective padding for sports is designed for the purpose of spreading the force at the point of contact over a wide area and hence reducing the force on any point. For example, the boxing gloves can spread the force of the striking fist over a much larger area instead of concentrating the force over a small area. As a result, it is easier for a boxer wearing gloves to hit hard without hurting his own fragile hand. In other words, the boxer in gloves can hit his opponent much harder without injuring himself. This information also give us hints for the common type of injuries involved in a boxing flight. If you are wearing boxing gloves when you hit someone, the blowing force will be distributed across the front of the gloves. The usual consequence is the snapping back of your opponent's head. Since the chance for a boxer wearing gloves to hurt himself is smaller, he can hit his opponent more violently. So some people support the return to bare-knuckle boxing in order to reduce the violence and injuries involved in boxing. Although abandoning the use of gloves would result in more broken hands, but there will be less broken heads. Sports like soccer often leads to injuries which have caused tears and heartbreaks of many audience. However, it also joyful for the audience to see a great athlete overcome an injury and return to the field.

Title page.