Research HighlightsBACK
Finite-temperature critical behaviors in 2D long-range quantum Heisenberg model
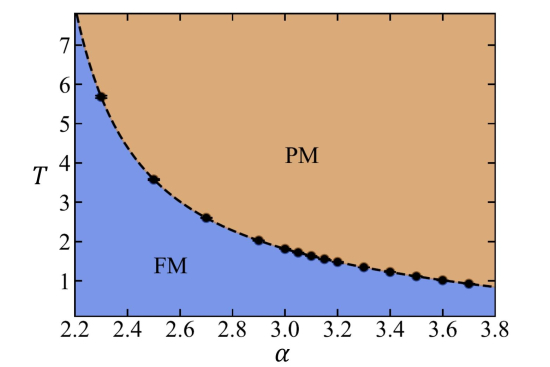
Fig. 1: Phase diagram of the 2D LR ferromagnetic Heisenberg model.
The Mermin-Wagner theorem states that spontaneous continuous symmetry breaking is prohibited in systems with short-range interactions at spatial dimension D ≤ 2. For long-range interactions with a power-law form (1/r^a), the theorem further forbids ferromagnetic or antiferromagnetic order at finite temperature when a ≥ 2D. However, the situation for a in (2, 4) at D = 2 is not covered by the theorem. To address this problem, we conduct large-scale quantum Monte Carlo simulations and field theoretical analysis. Our findings show spontaneous breaking of SU(2) symmetry in the ferromagnetic Heisenberg model with 1/r^a -form long-range interactions at D = 2. We determine critical exponents through finite-size analysis for a < 3 (above the upper critical dimension with Gaussian fixed point) and 3 ≤ a < 4 (below the upper critical dimension with non-Gaussian fixed point). These results reveal new critical behaviors in 2D long-range Heisenberg models, encouraging further experimental studies of quantum materials with long-range interactions beyond the Mermin-Wagner theorem’s scope.
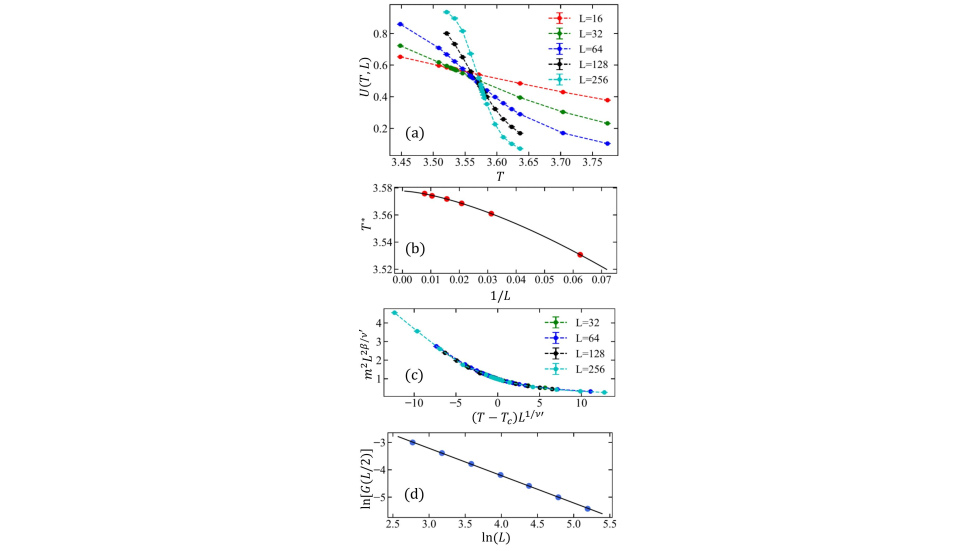
Fig. 2: The determination of the critical point and exponents at α = 2.5.
The research paper can be accessed at the following link:
https://doi.org/10.1038/s41535-023-00591-6




